Bitcoin Hunter Preview of Bitcoin Hunter About BitcoinHunter is software dedicated to find private keys of bitcoin addresses with balance.This software is free to download. Features Automatically generate private key and address to checkScrape Bitcoin directoriesAutomatically send found bitcoins to specific addressMultithreaded, lightweight. Type a Bitcoin BrainWallet PassPhrase: English BIP39 WordList: Random 39 Words Random 39 Words.

• Phrase Generator Bitcoin Private Key Free
• Phrase Generator Bitcoin Private Key
• Phrase Generator Bitcoin Private Key Checker
• Phrase Generator Bitcoin Private Key Generator
• Phrase Generator Bitcoin Private Keys

Making your own private key is a great feeling. I’m going to show you how, and keep it easy to follow. Most people will not go to the extreme of doing everything in this guide, but reading it will give some appreciation to how bitcoin storage works, the level of safety that is possible, and just how achievable it is with some planning and effort.

Most of it can be done without a computer, but towards the end, a computer is essential to get your extended xpub and wallet addresses. This really should be done on an air-gapped computer for maximum safety. This is how to make one. In 2020, it costs about $50 USD for all the parts.

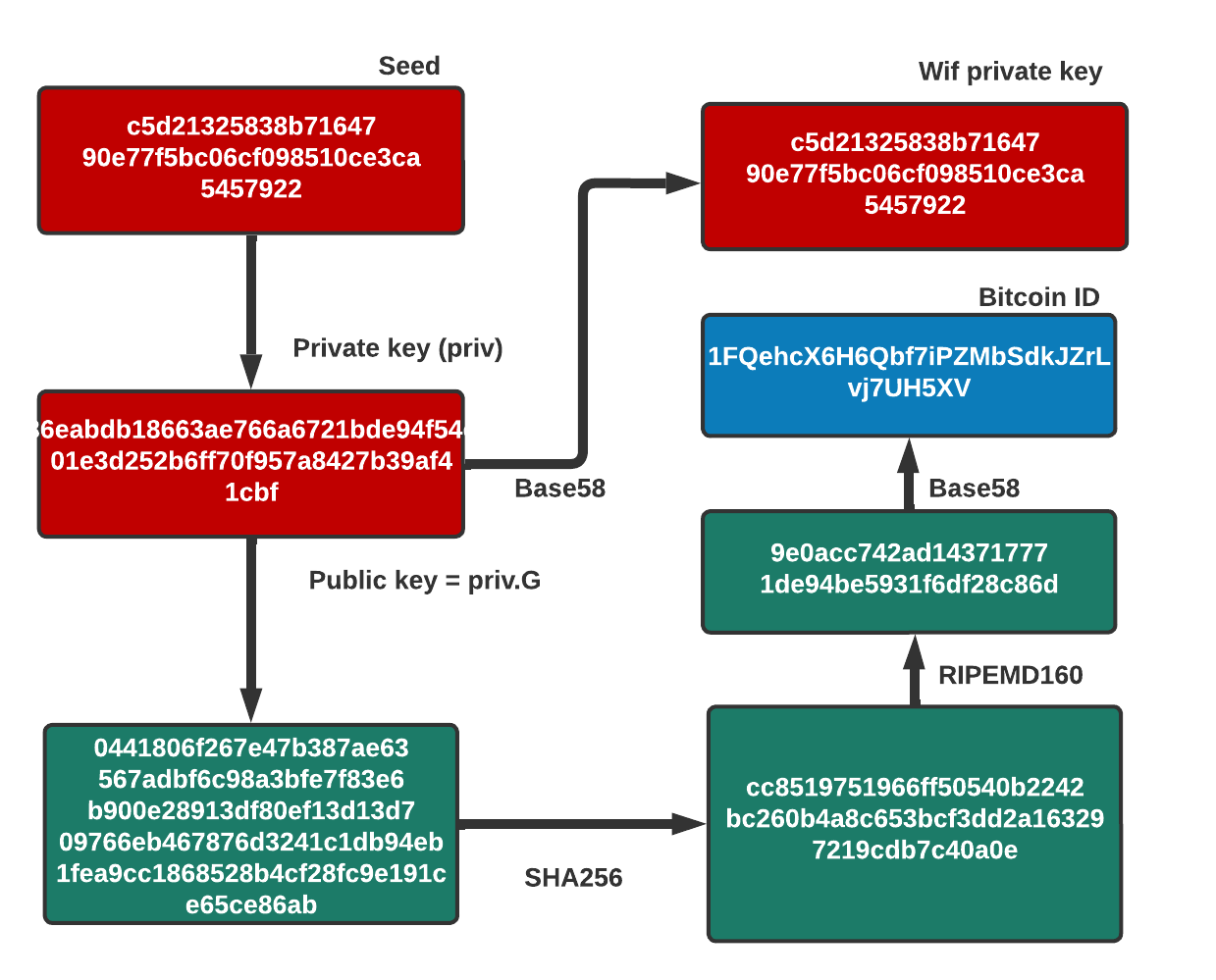
A Bitcoin private key is 128 to 256 bits long. Meaning 128 to 256 zero’s or one’s. You can pick them at random from your head, but it probably won’t be truly random. Maybe it’ll be fine, but I wouldn’t advise trying it.

These are the steps involved:

Step 1 – Generate a large binary number. I will explain the dice method to do this

Step 2 – Convert the binary number to words from the BIP39 word list

Step 3 – Calculate the final word, which is a checksum

Step 4 – Check the resulting xpub/zpub/Zpub and addresses from two independent sources

Step 5 – Repeat steps 1 to 4 to make several private keys (for making a multi-signature wallet)

If you want to back up your key to metal (to prevent loss in a fire) you can easily etch the binary key as shown in this video with a cheap engraving pen (writing words with a steady hand is hard, vertical and horizontal lines are easy).

STEP 1 – Generate entropy. The large number

The BIP 39 list of words are seemingly random words, in alphabetical order, numbered 0 to 2047. Each word represents an 11 bit number (eleven 0’s and 1’s). In 11 digit binary, 0 is 00000000000, and 2047 is 11111111111. This is not a coincidence.

Put in a different way, the numbers 0 to 2047 in decimal, fit into 0 to 11111111111 in binary.

The first word on the list is “abandon”, and codes for the number 00000000000. Word “ability” is next on the list and codes for the number 00000000001. The last word is “zoo” and codes for 11111111111.

24 words, each representing 11 binary digits, is a convenient way to write 256 bits of random data. Note, 11 x 24 is 264 though, the last 8 bits are not random, they make up part of the checksum (256 + 8 = 264).

If you want to use a 12 word seed, you can do that, but you make a key with only 132 bits (128 bits of randomness, and 4 more bits for the checksum. The procedure is mostly the same as for the 24 word version described here.)

Make 256 bits of data with dice:

You can do this with one die but it’s slow. You can use several dice at once. Here is how I made a sample private key, with 5 dice:

1. 5 dice are to be rolled together multiple times until 256 readouts are recorded.
2. Dice shall be read from left to right. If too close to call, read top to bottom.
3. A roll of 1, 2, or 3 records a zero.
4. A roll of 4, 5 or 6 records a one.

Here are my results for this example:

11100100111 11100111000 01011111110 10101001010 00010010000

01011100111 00100010101 11011001010 00100000101 01111100101

00110001010 11101100101 10101000101 01001001101 10111010101

01011011001 00010011111 01111000110 11001110011 01000011101

10111010000 01010000000 11001000010 101

Step 2 – Convert binary numbers to words

You can look up the binary numbers and find the word from a binary look-up table. The One linked is courtesy of @bjdweck from his “Rudefox” project. You can get the first 23 words this way. To get the final word, skip to the next step (checksum).

Alternatively, and preferably, you can look up from the original source, the BIP 39 words form the Github page. These words are numbered 1 to 2047, in decimal, not binary. The 11 digit binary groups from the dice rolls need to be converted to decimal, and then you look up the word.

To convert to decimal, you can use an online calculator, but we don’t want to put these dice rolls into an internet connected computer. This is a quick video (I suggest you watch at double speed) showing and easy way to convert binary to decimal manually.

Decimal Lookup Procedure

If we had a binary of 000000000, ie zero, then we would need the first word on the list. In the Word List from Github. This word is “abandon” and it is unfortunately labelled as word “1” instead of “zero”. So any number we convert from binary to decimal, we also need to add 1 to get the right “look up number” for this table.

Binary

11100100111

11100111000

01011111110

10101001010

00010010000

01011100111

00100010101

11011001010

00100000101

01111100101

00110001010

11101100101

10101000101

01001001101

10111010101

01011011001

00010011111

01111000110

11001110011

01000011101

10111010000

01010000000

11001000010

101

Decimal

1831

1848

766

1354

144

743

277

1738

261

997

394

1893

1349

589

1493

729

159

966

1651

541

1488

640

1602

NA

Decimal plus 1 & word

1832 top

1849 train

767 garlic

1355 power

145 bamboo

744 friend

278 cargo

1739 sun

262 camera

998 lake

395 course

1894 uncover

1350 post

590 endless

1494 rival

730 forest

160 become

967 juice

1652 solar

542 dry

1489 ring

641 exotic

1603 sign

NA (checksum)

For word 1, the decimal is 1831 on the list. If you look that up, you’ll get the wrong word because the list starts with 1 instead of zero. So add one to 1831, and look up word 1832. The word is “top”, not “tooth”

Once you make 23 words, you’ll have 3 digits remaining, which will be used for the checksum, next:

Step 3 – The Checksum

In this example the left over digits are 101. (For a 12 word seed, there will be a remainder of 7 digits)

Phrase Generator Bitcoin Private Key Free

Take all the digits from the dice rolls (256- which includes the 11×23=253 word digits, and the final 3 remainder) and get the SHA256 hash.

Next, take the first two digits of the resulting hash (they are hexidecimal, meaning each digit represents up to the value 16… 0 1 2 3 4 5 6 7 8 9 a b c d e f) and convert them to 4 digit binary.

You will have two sets of 4-digit binaries, so 8 binary digits in total makes the non-random component of the checksum. Add them to the random component (remainder of the dice rolls- those last three digits; in this example it’s binary 101), and you have 11 binary digits (8 non-random + 3 random). That makes the 24th word.

For a 12 word seed, you only need to take the first digit of the hash, convert to a 4 digit binary, and add that to the 7 digit remainder to make an 11 digit binary.

If you just guessed the final word, you can avoid the calculation to get the checksum. You simply guess until your wallet software accepts the checksum as valid. There are multiple possible checksums. Guessing a 12th word has a 1 in 16 chance of success. Guessing a 24th word has a 1 in 256 chance. If you guess, you replace the randomness from remainder dice rolls with randomness of guessing one of the several possible valid checksum words. A 12 word seed has 128 possible checksum words, a 24 word seed has four.

Procedure example:

Use an air-gapped Linux computer, and type this in the terminal:

echo 1110010011111100111000010111111101010100101000010010000010111001110010001010111011001010001000001010111110010100110001010111011001011010100010101001001101101110101010101101100100010011111011110001101100111001101000011101101110100000101000000011001000010101 | shasum -a 256 -0

This is “echo” followed by a space, followed by the binary number, a space, a pipe symbol, a space, “shasum”, a space, a hyphen, “a”, a space, “256”, a space, a hyphen, then”0″. That’s a zero at the end not the letter “o”.

The “-0” tells the hash function to treat the “0” and “1” characters for their binary value, not their printed ASCII characters.

• The printout of character “0” is actually 00110000. We want the value “0”.
• The printout of character “1” is actually 00110001. We want the value “1”.

This was my output of the hash:

845fb089a63394b6f1c0b7f1b9bdc7e1b3cc61d7fefc158c916a609a80afc56b

The first two digits are 8 and 4. The binary values, using 4 digits, are 1000 and 0100. (If you need to convert one of the letters, remember that the decimals for the letters are: a=10, b=11, c=12, d=13, e=14 and f=15.)

Adding these two new binary digits to the remainder digits of 101, we get: 10110000100. In decimal, this is 1412. Add 1 to 1412, and we get 1413. Look up word 1413 = “rack”

The word “rack” is the 24th checksum word.

The terminal in Linux (and Mac) keeps a history of your commands. This is dangerous to leave in the memory. Type “history -c” to clear the private key from the history.

Step 4 – check extended public keys and addresses

This also has to be on the air-gapped computer, so we are never typing sensitive information into a computer connected to the internet.

We are going to transfer data from an internet computer to the air-gapped computer by a USB pen drive. I’ll call this the “forward direction” of data flow. This is the weakest point of security; there is a theoretical possibility of malicious software being transferred (in the forward direction) from the internet connected computer to the air-gap computer, however, we NEVER bring the USB drive back to the internet computer (reverse direction), so no information is leaked away from the air-gapped machine. Data transmission in the forward direction, in the absence of any reverse direction, is still a weakness though; nothing is perfect, but this is pretty close.

Ideally, get a brand new USB pen drive, and format it. Then copy Ian Coleman’s webpage to the drive.

Insert the drive into the air-gapped computer, and open the web page from the drive. On a Raspberry Pi Zero, it runs VERY slow, just be patient.

You’ll see you can change the word number from the default of 15, to 24, and then enter your words.

Then, check the box “Show entropy details” – you can then see the zero’s and one’s should match your dice rolls. There is also a list of the decimal numbers corresponding to the words. And you can see the checksum binary listed separately.

Make an empty text file on the USB drive.

Click the BIP84 tab, to switch over to native segwit. Then copy the “account extended public key” (starts with zpub). Shown below, highlighted:

Scroll down a bit more and copy the first address (starts with bc1q) from the website, and paste it into the text file. This is to confirm the zpub creates the correct address on our second independent check later on.

Next we want to enter the seed words into an Electrum Wallet (on the air-gapped computer of course) to check that we get the same zpub and first address.

Open Electrum. Name your wallet and click next:

Choose “standard” wallet:

Then “I already have a seed”:

Enter your seed. This is safe to do because your computer is not connected to the internet.

You are unable to click next, because Electrum doesn’t recognise the seed. It doesn’t use BIP39 seeds by default. Click “Options” then check “BIP 39”:

Now the seed should be recognised and you can click Next. Then leave the default, native-segwit, for bc1 type addresses, and zpubs.

Then you can add a password to encrypt the file on the computer. Your wallet will load, but you can’t see the address list by default.

Go to “view” and “show addresses”:

Now a tab appears which lists your addresses. Check the first address matches the one you saved earlier:

Then go to the menu, “Wallet” and “Information”:

You will see the zpub. Check it matches with what you saved in the text file.

Zpubs

Next we want to create a Zpub (capital Z) associated with our seed, for multisignature wallets. Electrum creates this for us, but we need to verify it is doing it correctly. I had not found a way to do this with a web tool, and was using ColdCard Wallet’s export feature which is fine, but can be laborious. Thank you to @MinimalStructur who showed me this solution – It can be done on Ian Coleman’s BIP 39 online tool, it’s just tricky to find it…

After generating the seed, scroll down and select the BIP141 tab. This allows you to manually type in the derivation path. Do so as above, which is the Electrum default. Note that you must type it like that exactly. If you forget the apostrophes you’ll get the wrong Zpub.

You also need to modify the Script Semantics. Click the field with your mouse. It’s not easy to notice, but it’s actually a drop down menu.

You then should get an identical Zpub to what Electrum shows you.

Step 5 – Repeat steps 1 to 4

Repeat as often as you need to make the number of keys you desire.

Conclusion

If you followed the steps in this guide, you now have several private keys. Seriously well done! Store them securely. Consider memorising in addition to storing physically. This article explains my memorising technique for mnemonic seeds.

Having multiple private keys you generated yourself is very satisfying, very secure, and allows you to build a multisignature wallet. This article explains how to make a multisignature wallet.

Make sure, after going to all this trouble, you don’t leak your addresses to a public bitcoin node, and give away your privacy. Learn why and how to run a node, and connect your own fresh multisig Electrum wallet to that node, without ever connecting to a public node. Not even once. If you do, you have to start all over, and move your bitcoin to the new wallet. Painful.

In case you are feeling generous:

bc1qjwdcez7dc0wzjst4uum79v7zdqkyh6gr7d43a8

In various places in Bitcoin, it is important to generate secure passwords/passphrases. Security is especially important in Bitcoin because if your BTC is stolen, there is often no recourse. Bitcoin transactions cannot be reversed.

• 1Strength
• 4Using dice
• 5Using a computer

Strength

There are two very different use-cases for passwords in Bitcoin. The first and more common is an 'offline passphrase'. With an offline passphrase, something prevents an attacker from trying to guess your passphrase as fast as he might like.

Examples include:

• Website passwords. The website will rate-limit attempts on your password.
• Wallet passphrases. An attacker needs both the wallet file and your wallet passphrase.
• Hardware wallet PIN. An attacker needs both the hardware wallet and your PIN.

All of the advice you've ever heard about password security has been for the offline password use-case.

The second use-case is an 'online passphrase', where the passphrase is essentially the only thing protecting your BTC. In this case, your passphrase much be massively more secure than usual, and you can not rely on any password-creation advice you've ever heard.

For use cases that are vulnerable to a global passphrase cracking search, imagine that the entire world could be constantly trying to crack your passphrase, billions of attempts per second, all the time and with no restriction. This is not a normal situation outside of Bitcoin.

Examples of keys that could be cracked by a global search:

• The seed/mnemonic of an HD wallet.
• The passphrase on a wallet file that has become public, or that an attacker has otherwise gained access to.
• The input to a 'brain wallet'. (Warning: it is very strongly recommended that you not attempt to use a brain wallet.)

Example of keys that could be cracked by a targeted search:

• The passphrase on a wallet file that may become public, or that an attacker could gain access to.
• The input to a secure 'brain wallet' with e-mail salting, and an expensive Key Derivation Function.

Standards for offline passphrases

Between 64 and 80 bits of entropy seems reasonable. The password must be totally random (see later sections on generation). Hardware wallets have additional protections, and it's OK that they often allow only a short PIN.

This corresponds to the following password/passphrase lengths:

• Digits only: 20-25 digits
• Hexadecimal: 16-20 characters
• All lowercase or all uppercase letters: 14-18 characters
• All lowercase or all uppercase letters + numbers: 13-16 characters
• Mixed case letters: 12-15 characters
• Mixed case letters + numbers: 11-14 characters
• All standard keyboard characters: 9-11 characters
• Diceware words: 5-7 words
• Random English words (100,000-word wordlist): 4-5 words

Standards for online passphrases

Usually you don't have to personally generate an online passphrase. The most common case of an online passphrase in Bitcoin is the mnemonic for an HD wallet seed, but a good wallet should securely generate it for you (this is the several-word mnemonic that most wallets tell you to write down when first run), assuming it has not been tampered with.

In case you need to manually generate an online passphrase, 128 bits of entropy is required. The passphrase must be totally random (see later sections on generation).

This corresponds to the following password/passphrase lengths:

• Digits only: 39 digits
• Hexadecimal: 32 characters
• All lowercase or all uppercase letters: 28 characters
• All lowercase or all uppercase letters + numbers: 25 characters
• Mixed case letters: 23 characters
• Mixed case letters + numbers: 22 characters
• All standard keyboard characters: 20 characters
• Diceware words: 10 words
• Random English words (100,000-word wordlist): 8 words

Risks of automatic seed/passphrase generation

Automatic wallet seed/passphrase generation is only secure using:

1. Faithful wallet software: that has not been maliciously tampered with. If you haven't compiled wallet software yourself on a trustworthy computer running a trustworthy compiler, trustworthy source code is no guarantee for a trustworthy binary. See the Ken Thompson hack for details. Wallets with a deterministic build process (e.g., Bitcoin Core) are more resistant to attack.

1. Faithful RNG: An RNG (Random Number Generator) may be implemented in software, hardware or both. Wallet software relies on the security of the RNG, to generate your wallet's private keys securely. An insecure RNG may create wallet keys that can later be recreated by an attacker, by generating psuedo-randomness that would seem statistically indistinguishable from true randomness yet still be predictable to an advanced attacker. An RNG may become insecure as a result of malicious weakening or an unintentional mistake. This failure mode is common to any wallet generation procedure in which the true randomness of the source of entropy being used can not be verified.

1. Faithful hardware: software is executed by hardware. Unfaithful hardware may execute faithful software unfaithfully. This would be especially difficult to detect for computations where the final output is non-deterministic, such as an unfaithful hardware execution of Random Number Generator routines. The risk of such an attack is increased by the opaqueness of hardware implementation, and the centralized capital intensive nature of hardware manufacturing, making hardware companies more vulnerable to coercion, especially in undemocratic countries where most hardware manufacturing currently takes place.

For high risk applications, a pair of fair dice can provide a simpler, verifiably secure source of entropy.

How not to generate passphrases

Humans are really, really bad at generating passphrases on their own. Don't try it. If at any step in the passphrase-generation process your brain is being used to choose something at random or randomize something, then you're doing it wrong.

Do not take words out of a book or other work. The words must be absolutely random.

Do not use the xkcd password generation method.

Using dice

Dice can be used as one way to generate random numbers and passwords. However, in order to achieve security, you must use them in a certain way.

Secure dice

Casual dice for board games are not shaped perfectly, and will be somewhat biased toward certain numbers. Special casino dice are available which do not have this flaw.

The extent to which slightly-biased dice actually affect real-world security depends on the use-case. For the use-cases on this page, if the dice is random enough to not notice its bias when playing games, then it is probably good enough.

Generating passwords

To generate passwords, write down a list of acceptable characters, and sequentially number each character starting from 1. For example, if you want to generate a 4-digit PIN, you would create a list like this:

If you wanted to generate a password with characters in [a-zA-Z], you would create a list like this:

Now you need to figure out how many dice you're going to need to roll. Your dice should all have the same number of sides. If your character list has C characters, and each of your dice have S sides, then you need to roll log_S(C) dice, rounded up. For example, log₆(52) is about 2.2, which you round up to 3. So if your character list contains 52 characters, then you need to roll 3 6-sided dice.

Here, the dice are assumed to be numbered from 1 to S. If this is not the case, then you must create a system to translate the dice results into a range from 1 to S. For example, if you are dealing with 10-sided dice labeled from 0 to 9, then you can add 1 to the roll.

Roll the required number of dice and put them in a random order. Do not sort the dice from highest to lowest or anything like that. In fact, to prevent any personal bias from entering into the ordering, you may want to roll the dice and then put the dice into a line with your eyes closed.

Say that d₀ is the rightmost dice you rolled, d₁ is the second-from-rightmost dice you rolled, etc. Then the random number is:

1 + [(d₀ - 1) × S⁰] + [(d₁ - 1) × S¹] + [(d₂ - 1) × S²] + ...

For example, if we rolled 316 with 6-sided dice, this becomes:

1 + [(6 - 1) × 6⁰] + [(1 - 1) × 6¹] + [(3 - 1) × 6²]
= 1 + [5 × 1] + [0 × 6] + [2 × 36]
= 1 + 5 + 0 + 72
= 78

So our random character would be the 78^th character in the list.

Important: If your number is larger than you need, then you must totally reroll for this character. Do not try to 'wrap the numbers around' or keep only certain dice, as this results in a non-random distribution. (For the adventurous only: You can safely reduce the number of rerolls by pretending that the highest-order die has fewer sides. Eg. on a 6-sided die say that 1&4 = 1, 2&5 = 2, 3&6 = 3; or that 1&2&3 = 1 and 4&5&6 = 2. Still multiply it by the appropriate power of 6, not 3 or 2. But the die must be evenly divided, you must ensure that the maximum possible value is still greater than or equal to the highest-value character, and you must use the exact same treatment of the high-order die throughout the generation process.)

Important: There are a variety of different ways to get a random number from multiple dice, but they are usually non-random. For example, adding dice would be very non-random. The above method ensures a random distribution if the dice themselves are random and if they are ordered randomly.

If the password is L characters long, then password has log₂(C^L) bits of entropy.

Generating passphrases

As above, but use a list of words instead of a list of characters.

Note that there is a risk when acquiring your wordlist of an attacker giving you a wordlist that has duplicated or highly similar words. For example, the wordlist might look like it contains 1 million words, but actually be the same 1000 words repeated over and over again. Or all of the words might have an 'o' in the fourth position. Etc. This can cause you to significantly overestimate the security of your passphrase. Therefore, you must acquire your wordlist from a trusted source.

Generating keys, seeds, and random numbers (Advanced)

This section is mainly intended for programmers and advanced users.

Warning: it is considered unsafe to directly handle Bitcoin keys, as doing so is error-prone, and often causes people to send BTC into oblivion.

If you want to generate a large number for use as a key or seed, you can do the following.

First, decide how many bits of security you want. 128 bits is probably secure for most things. We will call this value B.

Next, roll log_S(2^B) dice, rounded up, where S is the number of sides per die. For example, with 6-sided dice you would need to roll 50 dice. Put the results right next to each other in a string of text, so for example if you roll 3, 2, 5, 6, 1, you'd start your string as '32561', and then continue on for a total of 50 digits. If your dice have enough sides to result in two-digit numbers, put a leading zero in front of single-digit numbers.

Then hash your string with a command like echo '32561...' |sha256sum. The resulting hash is your random number. If you want a 128-bit or 512-bit number use sha128sum or sha512sum, respectively. If you want some in-between number of bits, use the next larger hash size and then cut off the number where you need it.

You can generate any size of random number by combining the outputs. For example, let's say that you want 768 bits of randomness and for some reason you can only use sha256sum. You can do this like:

Then concatenate all of those hashes to get your final random number. In this example the result is cf6a25b...52b855.

Important: When generating a stream of random numbers like this, you have to put your source entropy back in at each step.

Phrase Generator Bitcoin Private Key

If you want to generate a number in a range with a range size that is not a power of two, choose the next-largest power of two and select the correct number of bits based on that. If the resulting number is too large, discard all of those bits and grab new ones from the endless stream of random bits. Do not use the modulo operator, as that introduces a bias. For example, if you want to generate a number from 0 to 9 (range size = 10), select the next-higher power of 2, 16. If your random stream starts 0xA52F..., grab 4 bits (log₂(16) = 4), giving 0xA = 10. This is outside of the range, so discard those bits and move onto the next 4 bits, 0x5 = 5. This is in the range, so the final result is 5.

When generating raw Bitcoin private keys: Although extremely unlikely to occur with a random 256-bit number, Bitcoin private keys cannot be equal to 0 or greater than to 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364140. When generating a Bitcoin private key, you should check that these conditions are met; if not, reroll the private key. Some software might allow you to use these invalid private keys, but doing so would be insecure.

Using a computer

Computers are good at generating secure random numbers, but you have to be careful to use the right commands. A lot of commands, programming language features, and snippets that you'll find online will give insecure random numbers which look random, but are predictable. For example, the C rand function, the Python random module, and the Windows %RANDOM% variable are all insecure random number sources.

Do not get your passwords from anything in a Web browser, even if the page says that it's using purely client-side JavaScript

Phrase Generator Bitcoin Private Key Checker

Linux

There are many different packages for generating random passwords/passphrases on Linux, but none of them are installed by default on all Linux machines, so we will provide a method that uses more standard commands. If you would like a more concise and easy-to-use command, we recommend installing an actual password generator package.

The following command will generate a 20-character random password:

Change -head-count=20 to change the password length, and [a-zA-Z0-9]|[[:punct:]] to change the character set. Note that this command will never use characters outside of ASCII, even if your grep pattern would select such characters.

To generate a passphrase made of words, create a file called words with one word per line and Unix-style line endings, and run:

Change -head-count=7 to change the number of words.

Note that there is a risk when acquiring your wordlist of an attacker giving you a wordlist that has duplicated or highly similar words. For example, the wordlist might look like it contains 1 million words, but actually be the same 1000 words repeated over and over again. Or all of the words might have an 'o' in the fourth position. Etc. This can cause you to significantly overestimate the security of your passphrase. Therefore, you must acquire your wordlist from a trusted source.

Windows

Phrase Generator Bitcoin Private Key Generator

KeePass includes a password generator, though not a word-based passphrase generator.

(If anyone knows of some better ones, edit this page to add it.)

Phrase Generator Bitcoin Private Keys

See also

• zxcvbn - A realistic passphrase strength estimator